


 |
| Hlavní stránka |
| Škola |
|
Doprava |
|
Táboření a kluby |
|
Reportáže |
|
Fotografie |
|
Témata |
|
Ostatní |
|
Rozcestník |
|
Ke stažení |
|
Sázky |
|
Návštěvní kniha |
|
Kalendář |
|
Kontakt |
 |



|


|
t-test |
Studentův t-test pro určení shody průměrůt-test je nejstarší statistický test pro posuzování shody výběrové veličiny (průměru) se známou zadanou hodnotou, resp. v upúravené variantě shody dvou výběrových průměrů. Test předpokládá normální rozložení pravděpodobnosti náhodné veličiny a využívá pro určení míry pravděpodobnosti, s jakou se porovnávané hodnoty shodují, tzv. Studentovo t-rozdělení. PrincipPrincipem t-testu je výpočet testového kritéria (veličiny) t ze znalosti střední hodnoty (průměru) realizací náhodné veličiny, jejich počtu a rozptylu. Pro základní jednovýběrový t-test (porovnávání průměru realizací se známou/předpokládanou hodnotou) má testová statistika t následující předpis: 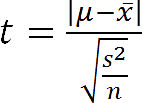
Předpoklady
Výpočet
Ukázka v jazyce RNejjednodušší variantou bez zadávání dalších paramtrů je jednovýběrový (tj. známe jen jednu sadu realizací, kterou porovnáváme se zadanou hodnotou) oboustranný (skutečná hodnota může být vyšší i nižší než zadaná hodnota t-test. Následující ukázka popisuje využití funkce t.test se zadáním jedné sady realizací (čísla od 1 do 5) a zadanou hodnotou 4. Výsledná p-hodnota je 0,2302 což (dle očekávání) odpovídá velmi nízké hladině významnosti pro ktrou lze vyloučit nulovou hypotézu (s pravděpodobností chyby 23 % lze očekávat, že hodnoty se od sebe liší). t.test(c(1,2,3,4,5),mu=4) Článek na dané téma si můžete přečíst rovněž na serveru Správným směrem.cz Článek ze dne 23. 6. 2014 byl naposledy upraven dne 23. 6. 2014 a zobrazen celkem 35898×, naposledy dne 11. 2. 2026 v 14:15.
|
||||||||||||||